출처: Stanford CS231n 2017
CS231N 2017
www.youtube.com
*참고 https://github.com/visionNoob/CS231N_17_KOR_SUB
GitHub - visionNoob/CS231N_17_KOR_SUB: CS231N 2017 video subtitles translation project for Korean Computer Science students
CS231N 2017 video subtitles translation project for Korean Computer Science students - GitHub - visionNoob/CS231N_17_KOR_SUB: CS231N 2017 video subtitles translation project for Korean Computer Sci...
github.com
1. Backpropagation(역전파)
- 인풋에 대한 gradient 를 구하는 과정
- 즉 인풋이 아웃풋에 어느정도 영향을 미치는 정도를 구하는 것
- 이를 위해 중간 매개변수인 q를 도입
- $q$를 $x$에 대해서, $y$에 대해서 편미분하면 각각 1이 나옴
- $f$ 또한 편미분하면 $z$와 $q$가 구해짐
- 아래와 같이 fp(forward path) 를 구할 수 있음
- 하지만 우리가 원하는 것은 아웃풋에 대한 인풋($x, y, z$)의 영향력
-즉 $df/dx, df/dy, df/dz$ 를 구하고 싶은 것

- 오른쪽에서 왼쪽으로 진행하는 것을 BP(backward path)라고 하는데, 이 방향으로 역전파를 구하여 loss를 갱신하는 방법을 사용
- $df/df$ 부터 구해보면 자기 자신을 구하는 것이므로 $df/df = 1$

- $df/dz$ 는 미리 구해져 있으므로 q 이므로 3
- 3이란 것은 무엇을 의미하냐면 z가 h만큼 변할 때 f는 3h 만큼 변하다는 뜻

- $df/dq$ 도 미리 구해져 있음
- z이므로 -4
- 즉 z가 h만큼 증가할 때 f 는 -4h 만큼 감소한다는 뜻

- $df/dy$ 를 구할 댄 Chain rule 를 이용하여 구함
- Chain rule 이란 약분할 수 있는 형태로 식을 변형 시키는 것
- $df/dy = df/dq * dq/dy$
- 즉 $df/dy = z * 1 = z = -4$

- $df/dx = df/dq * dq/dx$
- 즉 $df/dx = z * 1 = z = -4$

- 다음 layer에 대한 영향력, 즉 z에 대한 $x,y$ 의 영향력을 $dz/dx , dz/dy$ 라고 할 수 있는데 이 gradient를 local gradient 라고 한다.

- 다음 레이어에서 역전파를 통해 전달되는 gradient($dL/dz$) 를 global gradient 라고 한다 (이 때 L은 Loss 라고 생각하면 될 것 같다)

- 즉 출력(L)에 대한 입력(x) 의 영향력은 chain rule을 통해 표현 할 수 있다
- $dL/dx = dL/dz*dz/dx$ 이다.
- 근데 자세히 보면 이는 local gradient($dL/dz$)와 local gradient($dz/dx$)의 곱으로 표현 될 수 있다.
- 즉 영향력은 출력층의 local gradeint와 global gradient의 곱으로 표현할 수 있는 것이다.
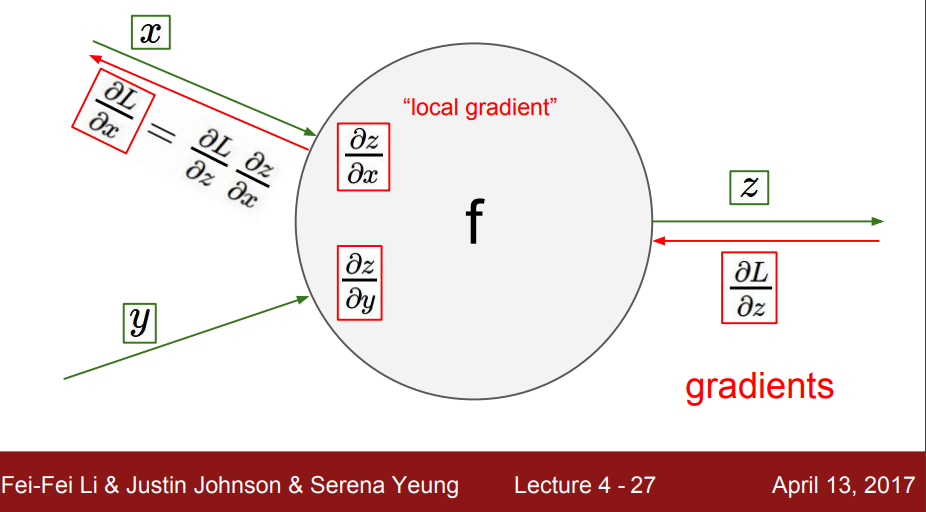
- y 또한 같다.

이러한 원리로 역전파가 진행된다.

- 예를 들어 설명해보자
- 아래와 같은 modul이 있다

- 이를 쉽게 설명하기 위해 역전파 원리를 설명할 때 $x$가 $a$,$z$가 $L$이라고 가정해보자.
- $L$에 대한 $a$ 의 영향력을 구하기 위해서 $dL/da$를 구해야 하는데 아까 언급했었던 Chain rule 방식을 사용한다
- $dL/da = dL/db * db/da$ (b는 계산을 위해 도입) 이것이 local gradient 가 됨
- 여기서 local gradiet 는 $dL/da = -1/x^2$ 에 $x = 1.37 $ 대입
- local gradient 는 $-1/1.37^2$ 이다.
- gradient 는 위에서 언급했듯이 local gradient 와 global gradient($dL/dL = 1$) 의 곱이라고 했으므로
- $(-1/1.37^2) * 1 = -0.53 $

- local gradient 는 $c + x $ 의 미분이므로 1이다.
- grobal gradient 는 방금 전에 구한 -0.53 이다.
- 즉 gradeint 는 이 두개의 곱이므로 -0.53 이다.

- local gradient 는 $e^x $ 의 미분 값이 $e^x$인데 $x =1$ 이므로 local gradient는 $1/e$이다.
- grobal gradient 는 방금 전에 구한 -0.53 이다.
- 즉 gradeint 는 이 두개의 곱이므로 $(1/e)(-0.53) = -0.2$ 이다.

- local gradient 는 $ -x $ 의 미분값이 $-1$ 이므로 local gradient는 $-1$이다.
- grobal gradient 는 방금 전에 구한 -0.2 이다.
- 즉 gradeint 는 이 두개의 곱이므로 $(-1)(-0.20) = 0.2$ 이다.

- 이 부분도 위와 동일
- $x+a$ 를 미분하면 1 > local gradient = 1
- global gradient = 0.2
- gradeint $ 1 * 0.2 = 0.2$
- w2 와 위쪽 gradient 는 모두 0.2가 됨

- 다 같은 원리기 때문에 계산 과정 생략하겠음

- sigmoid function 은 시그모이드 함수 부분임
- 시그모이드를 미분값은 자신으로 설명되는 식임
- 아까 시그모이드 영역에서 역전파를 통해 0.2를 구하기 까지 엄청난 과정을 겪었는데 그럴 필요가 없음
- local gradient 는 시그모이드의 미분이고 grobla gradient는 1.00, $x = 0.73$ 이라고 생각하고 계산하면 되는 것임
- local gradient : $(1 - 0.73)(0.73)$ 이고 grobal gradient 는 1 이기 때문에
- gradient 는 $(1 - 0.73)(0.73) * 1 = 0.2 $ 인 것이다

- 더하기 layer : 자신의 gradeint 를 전달하는 역활
- max gate : 큰 것의 local gradeint 는 1이고, 작은 놈의 local gradient는 0이 될 것이기 때문에 큰 것만 곱하기 1을 하게 되는 결과에서 이것은 여러 개 중에 하나만 취해준다라고 함
- 곱하기 gate : $f = qz$ 라고 할 때 $df/dq = z$ 가 되고 $df/dz = q$ 가 된다. 즉 locla gradient는 곱하는 쪽의 반대쪽이 되기 때문에 switcher 의 역활을 한다고 함

- 입력이 4096 이고 출력도 4096 일 때
- 자코비안 행렬의 사이즈는 4096x4096이 될 것이다.

- 이 때 $f(x)$ 는 4096x4096 크기의 행렬이지만 대각행렬로 이뤄져있을 것이다.

- 그리고 미니배치 형식으로 한 번에 100개씩 전달하기 때문에 $f(x)$ 실질적으로는 409,600X409,600의 대각행렬로 구성되게 될 것이다.
2. Neural Network(NN)
- 이전에 선형함수에서 배웠던 $f$ 는 $W,x$ 가 곱해진 형식으로 이뤄짐
- Neural Network 는 두 개의 layer가 있다고 할 때 첫 번째 layer에서 출력($W1x$)을 입력으로 받는 두 번째 layer(이 layer의 출력값은 $( W2max(0,W1x) )$로 구성돼있는 Network이다.
-입력으로 3072개를 받고 이것들과 W1이 곱해져서 계산된 후 hidden layer 에 100개의 출력을 전달함.
- hidden layer 에서 100개의 입력을 받고 W2와 곱해서 계산한 후에 10개 클래스를 출력

- 3개의 층도 가능

- 활성화 함수
- 렐루가 가장 많이 사용

- 가중치가 있는 layer만 갯수를 세준다.

-마지막 nn은 기본적인 내용들이라 생략함
